Triple Integral - Calculus Ang Tatlong kabuohang Sakop

Triple Integral Calculus "Ang Tatlong Kabuohang Sakop"



Introduction:




Objectives:



Methodology:








Remarks:



Conclusions:

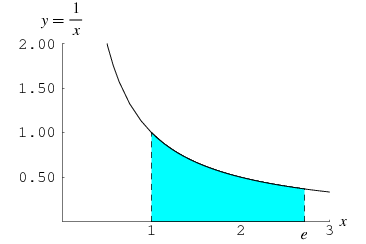
Numerong walang payak na bilang (e at pi )

Kasaysayan

Natural logarithm

'e'
Ang numerong 'e' ay isang numero sa matematika  na may dami na  di karaniwang dami  dahil sa ang natural na logarithmo nito ay may bilang na isa. Ito ay may bilang na halos 2.71828 , o dalawa na may di payak na kabahagian o kwake. Ang sukdulan ng kalkulasyun  (1 + 1/n)ⁿ   ay  n  o nangangahulugang mahabang pagbibilang patungo sa walang hangan pag hahati. 

 Sa isang literal na halimbawa ,makikita sa baba ang  resulta ng bilang  kung papaano hatiin ang isa bilang ng simula sa isa hangang sa dulo ng walang katapusang pag hahati

= 1  + 1/2  + 1/3 + 1/4 + 1/n

n  kung saan mang numero ito sukdulang ang pag hahati ay gagawin

kaya ang kalalabasan  1 + 0.5 + 0.3 + 0.25  (..dito pa lang meron na tayong 2.05, cge ituloy natin) + 0.20  + . +.. + 1/10000000000000000000000  + cge dagdagan pa natin dito may forever!

= 2.71828

Gamit ng 'e' sa realidad ng buhay

Ang isang halimbawa nito ay ang tubo na nakukua sa interest ng mga interest -isang usapin sa puhunan at dami ng kita sa pag papautang ng banko.

Ang isa pang kahalagahan nito sa buhay ng mga syentista sa computer ay magbigay ng ambag sa

kung anong bilang na ang e at gaano na kadami itong hinati. Simula mga dakilang matematiko ng panahon sa unang kwaki sa kalkulasyun ni Bernouli , 205 na hating bilang ni Willaim Shank, sa 2010 bilang hati ni John Von Neuman at 11600 ni Esteve Wozniak na kasama sa nag tatag ng Apple Computer. Hangang sa kasalukuyan patuloy pa din ang pananaliksik sa  tumpak ng bilang ng e, at katuwang na natin ang mga computer para harapin ang hamon na ito.


Reference: 
http://www.wikipedia.com

Differential Calculus usapin sa Palayan

Isa sa mga nakakatuwang napag uusapan minsan sa baryo ay ang Differential Calculus, pero malinaw naman na ang mathemathical term na ito ay  lingid sa talatinigan ng kanilang bokabularyo.

Nakaugalian na ng mga magsasaka sa ating baranggay ang mapag usapan ang lagay ng kanilang mga pananim sa palayan kasama na dito ang pagpunla ng binhi,pagpalago ng tubo ng palay o  mga takda sa pagpa patubig o permiso sa pagpapabukas ng  irigasyun ,pagapas ng damo at kailangang abuno,minsan kung may masamang panahong darating na  bagyo na may dalang pagbaha nag kakaroon sila ng seryusong pag ta-tanya ng mga gagawin.

Likas na sa ating mga abang mag sasaka ang magkaroon ng malalim na analisasyun sa mga hakbangangin pag lalaanan nya ng panahon .Ang nakakatuwa sa di natin inaasahang senaryo

ay maitutulad natin ang kanilang mga metodolohiya o teknik gamit ang kalkulasyun sa Differential Calculus. At bakit?

Bago pa man  mag tanim ng palay ang mga mag sasaka ay nag lalaan na sila ng binhi na papalaguin sa kwadro sa loob ng palayan.Ito ang kanyang naturang kwentada at kalkulasyun

Una, kailangan nyang  punuin ang dalawang tig-iisang metro kwadrado na luwang para sa binhian ng palay, at kailangan sakto ito dahil masasayang ang palay na gagamitin. Bilang nya din kung ilang bahagi ang laman ng  sako ng palay na sasaktong  patubo sa dalawang parang o  depende sa dami.

Pangalawa, tantyado at exacto ang kalkulasyun nila ng panahon para sa pagusbong ng binhi ay hindi ito lampasan ng tubig sa panahon ng pagtubig.

Pangatlo,simpleng haba ng pisi o lubid naipapakita na lamang sa metro kwadrado ng binhi ay pasok pa ang stratihiya sa Differential Calculus, halimbawa sa sampung metrong bakud sa binhi  ng lubid at para walang sayang , ilang piraso ng pag puputol ang kinakailangan o sasakto ba ang haba ng pisi at kung man ilan ang mada dagdag. Para sa lahat di sanay itong abang mag sasaka natin gawa ng sa layo ng palayan sa kabayanan ay walang puwang ang kamalian o ulit at mali at sayang din ang pagod at gastusin mapunta nalang sana sa susunod na abuno.

Bagaman lingid na sa kaalaman ng lahat ang ganitong senaryo sa baryo , ay di ko pa din malilimutan ang minsang napag uusapan nila. "Poko Mas Ominus"  ,kumulang o sumobra ay mga salitang kalabisang napag uusapan nila para i analisa ang mga bagay na may bilang o dami o antas ng kalkulasyun sa palayan o bukirin.

Metro kwadrado ng binhi

Ipalagay natin na ang sitwasyun ng kalkulasyun nito ay tumpak sa kagagamitan ng Differential equation . At bakit nga ba naging diperensya? Simple lang ang sagot ang pinaka sukat man o bilang ang pinag uusapan dahil sa ito ay humahantong sa dalawang resulta ng sukat o bilang.

Ipagpatulad natin ito sa pag alam ng pinakamalaking lawak ng lugar na pwedeng pag tamnan ng binhi at ang kakailanganing bakud para dito.

Halimbawang may nakalaan lang ang nasabingmag sasaka ng tatlong daang piye (300 ft) kalawak na bakod.Ang tanong anong sukat ang pinaka malaki para sa lawak ng pagtataniman ng binhi?

Ipagpalagay na natin ang pag tutulad na ang pinaka malaking lawak ay may kalkulasyun o sukat sa nasabing dalawang sukat ang pahaba("y" ) at ang pahalang ('x')

I) Sa natural na lawak ang sukat ay  Lawak (A)= 2L * 2W , sa ibang definisyun ang nasabing lapad at haba na kayang buohin ang lawak ng lugar

II) Palawigin pa natin ang inpormasyun hingil dito , ang naturang pag babakud ay may pitong baha-bahagi.Ito ay,

300 = x + x + x +x + y +y +y

300 = 4x + 3y

III) Sa naturang pag tutulad ay mababalangkas natin na ang isang pahaba (y) ay may may kalkulasyun  na tual ng..

IV) Alamin natin ang sakop ng pag tutulad , sa pag susukat na ito, hindi pwedeng maging kulang o negatibo ang  pahalang ('x') na parte ng bakod.  Sa anumang sagot na pwedeng makuha sa pahalang ('x')  ay 300 hahatiin sa apat (4) o kaya hahatiin sa pitumput lima  (75). Opo naman wala kasi ito sa realidad  (ano ba kayo walng invisible na bakud kulang pa kaya sa wala (0)?). Sa makatuwid ang sakop lang ng kalkulasyun  para malamang ang pahalang ('x') na bakod- poko mas o minus, hihigit o kululang  0 ≤ x ≤ 75. Yan ang posibleng diperensya...

V)  Hanapin natin ang maaring maging sukat ayun sa nakalaan lang na bakud ayun sa lawak ng lugar na pag bibinhian, A(x)  di pwedeng lalampas o kulkulang sa pagitan ng  (0, 75). Kaya ipag palagay na nating  makipot o walang pag susukat sa 'x'  pahalang (ipagpapalagay lang) wala  (0-zero). Tingnan natin ang kalkulasyun. 

sa kadahilanang ang  A′ ay may pag tutudlas sa lahat ng sukat na pwede sa pahalang , 3.75 ay ang sagot  na sukat

VI) Suriin po natin ang pag tutulad sa pahalang na sukat , 37.5 at ang hanganan ng puwang ng , 0 and 75.

VII) Palagi nating tatandaan na sa pag susuri ng pagtutulad  ang hanganan ng puwang o limitasyun ang mga pangunahing alituntunin lamang sa pag hanap ng tiyak na sagot nito. Ang Minima o Maxima , o humigit ba o kumulang sa naturang sakop lamang ng tinitiyak na sagot nito maging bilang  ng dami o sukat ng laki.

Sa ating tinalakay ang kalakhan ng lawak ay     is 3750, and thus, an x-value of 37.5 feet maximizes the corral’s area. The length is 2x, or 75 feet. The width is y, which equals ...dahil sa ang pinka mahabang  pahalang ay 37.5 piye(ft) sa nakatalagang 300 piye (ft)  na pangbakud lamang . Ang  dalawang pahalang sa mag kabilaan ay 2X o sa kabuohang 75 piye (ft). At ang lapad ay ('y') na may tulad sa kalkulasyun o relasyun sa pahalang ('x') na...

IV.5)   Kung ating ihahalili ang bilang ang 37.5 piye(ft) sa pahalang ay reresulta sa

o singkwenta piye (50ft)  na habang palapad

Sa makatuwid ang mag sasaka ay makakabuo ng  75 foot by 50 foot  , na may lawak na 3750 piye kwadrado .

Konkulsyon:

Sa realidad ng sitwasyun na ito  gamit ang Differential Calculus malamang di literal na teknolohiya ito ng mga magsasaka,subalit ang nasabing pamamaraan ng ganitong kaalaman ay nag bigay sa kanya ng tamang sukat at walang aksya sa mga nakatalagang gagawing pangbakud. Sa ating nasaksihan

di lang natugunan ang pinaka malaking lawak ng espasyo para sa bakud, bagkus nalagyan pa nating bakud ang gitna. Sa kadahilanang kung walang bakud sa gitna ay magkakaroon lamang ng lawak o kabuohan laki  na  3600 square feet at 3673 square feet.  . Kaya sa naturang pag susukat mahalagang malaman ang sukat na sakto at walang sayang na gamit o kaya bakud na sa ibang pagkakataon ay humantong sa pag kalugi o pagka aksaya ng pera o puhanan sa pag tatamin sa palayan o bukirin.

Gamit ang Calculus sa pag papadami ng punlaan ng Palay(Video)


Maraming Salamat.

E^3

Ang Differential Equation sa Usapang Kanto

Mga pangunahing pag tatalakay patungkol sa Differential Equation:

Mapapansin natin  na madaming antas ang  pag susukat o pagbibilang ng mga anumang bagay bagay. Maaring ito ay sa abot lang ng ating mga daliri, maari ding mas malalim pa at gagamitan ng  kaalamang  may kumbinasyun ng dalawa o mahigit pang sistematikong  pag susukat o pagssuri ng bilang. Bagaman sa traditional na kasanayan,mayroon tayong inaasahang sagot na  payak ,buo o kabahagian lamang ng pinag uuspang bilang. Halimbawa, pinag hating dalawang  kilong bigas ay may payak na bilang, o kaya  kung hatiin sa lima ay  mag kakaroon ng  payak at pwakeng  sagot .Isang libong apat-napong kadaming aklat ay mag kakaroon ng buong sagot na apat napu na isang libong uri ng bilang patungkol sa aklat. Ang ganitong klaseng pamamaraan sa traditonal na pag susukat o pag bibilang ay di na kaila sa ating lahat, sa katunayan ay bukas ang kaalamang ito sa lahat ng tao aral man o hindi.

Sa isang punto ay marami pang mga bagay na kinaka kailangan ang pag susukat o pag bibilang na kung gagamitan natin ang nakaugaliang pamamaraan ay baka di natin makuha ang tiyak at tumpak na sagot. Dahil sa ang mga bagay na ating pag uusapan ay literal na di natin nakikita o walang katiyakang  dami ay mawawalang saysay ang payak na bilang. Halimbawa ay ang dami ng buhangin o dami ng bigas bagaman nabibilang ay di ankop sa pag susukat ng bagay. Isa lang itong halimbawa na kailangan natin bumaling sa isang sistema ng pag susukat yan ang kanilang timbang , sa ganitong kaparaanan ay nakukuha lang natin ang kanilang bilang sa proporsyun o kalkulasyun ng  bigat. Isa pang halimbawa  sa pag alam naman sa timbang ay pwede din ibaling sa relasyun ng dami,dahilang mahirap timbangin ang toneldang bato, subalit kung ang isang maliit o malaking piraso ng uri ng bato ay may timbang , sa loob ng isang malaking track kung saan maiimbak ang bato sa luwang  ng lalagyan ay makakalkula natin ang bigat nito.

Sa mga nasambit na pahayag ay ipinapaliwanag lamang  ang pagkakaroon ng bilang o pag susukat
na naiiba sa traditional na pamamaraan. Halimbawa sa isang katanungang iuugnay ang bilang at bilis para makuha ang layo o haba .

Isang  halimbawa ay.
Ang kutsero sakay sa kalesa ay nag papatakbo ng kabayo sa bilis  na apat napong  metro sa isang segundo at  sa bawat segundo na pagtakbo nito. Ang tanong gaano kalayo ang mararating ng kutsero pakalipas ng walong segundo sa naturang bilis na patakbo.

Ipalagay natin   dS/dt = 40t  ; kung saan ang  S(t) ay ang distansya sa metro sa takda ng  dt o pagbabago ng segundo /pahanahon, at ang t sa panahon ng segundo. Kaya ang hahanapin   ay layo makalipas ang 8 segundo..
  S(8)  = (?)metro 

Ang solusyon:
=>    dS/dt
= >   dS/dt = 40t
=>    dS = 40t x dt
=>    dS(t) = Integral { 40t * dt } + C; Integral o kabuohang bilang umpisa sa unang segundo hangang sa 8 o walong segundo
=>    S(t) = ( 40t *t ) /2   + C ; ipinag palagay  nating may sobra o kwake sa distansya 
=>    S(t)   = 20 t^2  + C  ;

Dahil sa ang  pag  pag sukat  ay sa simula  na di pa umaabante ang kalesa
=>   S(0) = 20(0) ^2 + C ;   Ang C ay wala pang kwake
=> S(8) = 20* 8^2 + 0
 S(8)  = (?)metro
=>  S(8) = 1280 metro

Isang simple at madaliang solusyon para malaman ito. Ang kabuohang pagbabago gamit ang dalawang bilang o sukat ng bagay(layo man o bilis): una ay ayun sa simula ng pagumpisa at pnagalawa ay ayun sukdulan ng panahon. Maari ding ipagpalagay ang halimbawa na ang 40ft /s ay  may pinag-umpisahan na  o kauumpisa pa lamang. Ang distansya at bilis  sa makatuwid ay matutulad sa ganitong kalkulasyun..
=> (ds/dt + 40/dt)/2  , ay magiging 20 /dt  * 1/t
=>  (20 )8 * 8
=> 1280 metro , 
Ito lamang  ay sa kadahilanang may relasyon ang bilis , distansya at panahon sa iisang  naturing na pag tutulad   para makuha ang patas at parehas(average)  sa na pag-babago sa bilis. 


Isa pang halimabawa gamit ang  pagsusuri sa pag lubo ng papulasyon:
Ang isang papulasyun ay ipinapalagay ang  pag lubo na  may  limang ma-isisilang na sangol sa bawat isang daang dami ng  tao at ito at sa bawat paglilipas ng isang taon. Ang tanong gaano katagal na panahon ang aabutin para ang kasalukyang dami ng papulasyon ay ma-dodoble?

  Ang solusyun:     Ipag palagay na nating na ang  initial o unang dami ng tao ay nag simula sa P0 at isipin na nating sa pag lipas(pag bago)  ng dT  panahon ay ganito na ang bilang o dami  P  

Ang pagbago ng Papulasyon  =  (5 maisisilang )P      o     dP  =   P           
Ang pagbabago ng Panahon      (bawat 100 na tao)           dT      20          

o kaya kung ating gagalawin ang equation o pag tutulad 
dP     = 1 dT  
P         20

..ipag papatuloy po ang talakayan...


Nakakatuwa at nakaka libang ang mga ganitong diskusyon lalo nat magiging karaniwang usapin na  lamang ito sa kanto. Naniniwala ang inyong linkod na kapag dumating ang panahong magiging bukambibig na ito ng karaniwang mamayan ay tiyak ang yayabong ang pag unawa sa anumang mga bagay na pagagamitan nito. Sa karaniwang kaalaman, sa palenke sa laro at lalo na sa eskwelahan. Sa panahong ito nakakatiyak tayong mas mataas na ang mga bagay na paguukulang panahon ng mg paham at enhinyero sa ating lugar . Subalit kailangan ding maunawaan ng mga guro na kailangan itong isalin at ipaunawa sa kamalayan ng mga karaniwang tao at bakit naman hindi ? Kung sa paglipas ng pahanon ito ay napaguusapan sa paaralan at tila nalilimutan na lang  abay san tayo pupunta at anong mangyayari kundi ang pag sayang ng panahon at pag palamuti lang sa mga kaalamang ito. Kung hindi sa baryo para saan kung walang output bat pa may Differential Equation malamang di sa numero ang diperensya bagkus sa mga nag aaral dito na nakakalimutang ipasa o ipaunawa ito sa mga taong di naman nasa silid aralan.

Hangang sa muli....

IS295B MIS (Information System Project Implementation)

                                                                         

Modified Carrier Robots-Xentrino Robot

Introductions:

First of all, this is a blog type of documentation, as technical papers will be submitted in the University for the  submission report of this project.This is  all about the design of  web based information system applicable of  gathering variable and discrete data.A data  that is important to represent status of a certain environment. This technology serves an indigenous initiative to support engineers,technician and system administrators for their N.O.C monitoring routine,this is appropriate to my current IT work place-Data Center . Yet, the said information has a general use to monitor and controls mechanical equipment, machines and robots. The final deliverable of the  project is to have an example of information system with prototypes (server,robot and tiny robots) to showcase an effective real-time monitoring and controlling things in a remote environment.

In my own application ,its title is "Information System Design of Data Monitoring System ,with collaborative Tele-Mobile Robots.The project will give a web-based display to monitor different data inside the servers-room such as humidity,light electricity,heat and etc.This is done by different transducers interface to a tiny single board computers.How ever , the project also involves a semi-autonomous group of robots roaming the rooms to boost data gathering in every area,particularly if its not with in the reach of the transducers attach to the stationary servers.

The said study took  almost three 3 semesters to finish the proposal, yet due to the technological design,learning curve,dilemma  and other problem outside its R&D period , it lasted more than three(3) years in the making. I would simply convinced myself that it is not  simply obtaining  diploma ,but  citing an experience that it is not just a walk in the park.

Requirements:
Source code : https://github.com/hi-techno-barrio/staticIS295B
Carrier Robots
Mini Server
Micro-Robots


Methodology:
Provide Technical Papers
Plan on the Drawing boards
Web Coding
Embedded Programming
Tweaking the mechanical Frame
Integration of all the design
Pilot Testing
Redesign Robots
Fine Tuning
Technical Documentations

References: photos,videos:

1) Original setup (Mcronbot,Chrisdonbot and Xentrinobot)

2) Temporary Range finder:Ultrasonic sensor per quadrant

3) Onboard computers and sensors

 

Remarks:



Summary:

Conclusions: